BLOG / RESEARCH - TRAVELING SALESPERSON PROBLEM

DIE LÖSUNG DES TRAVELING SALESPERSON PROBLEMS DURCH BESTIMMUNG EINES MINIMUM SPANNING TREE

Beitrag teilen

6 Min. Lesezeit

8. Juli 2019

Florian Diedrich

I n diesem Artikel¹ stellen wir einen Approximations-Algorithmus für das Traveling Salesperson Problem mit Dreiecksungleichung vor, das u. a. auch von PowerOpt gelöst werden kann. Der hier vorgestellte Algorithmus basiert auf der Bestimmung eines Minimum Spanning Tree (MST), der dann durch Traversierung und Abkürzungen in eine Tour überführt wird.

Zuerst erläutern wir einige aus der Graphentheorie stammende Begriffe und stellen kurz die verwendeten algorithmischen Komponenten vor. Nach einer Zusammenfassung weisen wir abschließend auf eine Verbesserung des Algorithmus hin.

1. EINFÜHRUNG: DAS TRAVELING SALESPERSON PROBLEM

Das Traveling Salesperson Problem (TSP) ist ein relativ anschauliches Optimierungsproblem aus der Tourenplanung. Die Eingabe besteht dabei aus „Knoten“ (die wir uns als zu besuchende Orte vorstellen können), die in einer „Tour“² besucht werden sollen. Je zwei dieser Knoten sind durch eine „Kante“ (eine Straße) verbunden. Zusätzlich sind positive Distanzen zwischen allen diesen Knoten gegeben. Das Ziel ist die Bestimmung einer Besuchsreihenfolge, bei der die insgesamt zurückgelegte Distanz minimal ist.

2. GRAPHEN, BÄUME UND DREIECKSUNGLEICHUNGEN

Etwas genauer besteht die Eingabe aus einem Graphen mit n Knoten, von denen je zwei durch eine Kante verbunden sind (Fig. 1). Die Distanzen zwischen allen Paaren von Knoten sind durch eine Funktion d gegeben, die z.B. in einer Distanzmatrix kodiert werden kann.

Fig. 1: Graph mit durch Distanzen gewichtete Kanten

Wir setzen voraus, dass je zwei Knoten durch eine Kante verbunden sind. Dies stellt sicher, dass überhaupt eine Rundreise existiert. Auf den ersten Blick scheint dies für praktische Anwendungen eine starke Einschränkung zu sein, da es beispielsweise nicht möglich ist, „direkt“ von Heikendorf nach Hamburg zu fahren – zumindest nicht in dem Sinne, dass dabei gar keine anderen Orte passiert werden.

Glücklicherweise haben wir aber unseren „algorithmischen Werkzeugkasten“ im Gepäck! Durch ein paar smarte Argumente können wir uns also überlegen, dass es sich nicht um eine echte Einschränkung, sondern um eine sinnvolle Ausschöpfung handelt:

1. Hat die Eingabe zwei Knoten, die nicht durch einen Pfad verbunden sind, so besitzt die Eingabe keine Tour. Ein Besuchen aller Knoten ist dann nur durch mehrere Touren möglich. Das Bestimmen der Zusammenhangskomponenten (die wir uns als isolierte Straßennetze vorstellen können) ist aber effizient mittels modifizierter Tiefen- oder Breitensuche möglich. Wir können dann darauf abzielen, für jede Zusammenhangskomponente eine eigene Tour zu ermitteln.

2. Besteht die Eingabe aus nur einer einzigen Zusammenhangskomponente, bei denen zwei Knoten a und b nicht durch eine Kante verbunden sind, können wir unterstellen, dass wir dennoch auf einem kürzesten Weg von a nach b fahren können. Diesen kürzesten Weg sehen wir dann als die fehlende Kante an. In einer ermittelten Tour wird diese künstliche Kante dann wieder durch einen entsprechenden kürzesten Weg ersetzt³ . Die Bestimmung der kürzesten Wege für alle Paare von Knoten ist z.B. durch den Algorithmus von Floyd-Warshall⁴ oder durch ggf. mehrfache Anwendung des Algorithmus von Dijkstra⁵ effizient möglich.

Unter einem Baum verstehen wir eine Auswahl der Kanten, die keinen Kreis enthält, aber zusammenhängend ist. Wir nennen einen Baum dann spannend für unsere Eingabe, wenn er alle Knoten enthält⁶. Wieder können wir die gesamte Distanz aller Kanten im Baum bestimmen. Einen spannenden Baum nennen wir dann einen minimal spannenden Baum, wenn die gesamte Distanz seiner Kanten unter allen spannenden Bäumen minimal ist⁷.

Das Problem der Bestimmung eines MST kann auch unabhängig vom TSP motiviert werden. Wir versetzen uns dazu etwa in die Rolle eines Städteplaners, der in unerschlossenem Gelände anzulegende Straßen planen soll. Dabei sind die Längen der potenziellen Straßen zwischen vorher festgelegten Knoten bekannt. Das Ziel ist dann, die Straßen so zu bauen, dass je zwei Knoten durch einen Weg verbunden sind – das zu erstellende Straßennetz soll aber aus Kostengründen eine möglichst geringe Gesamtlänge⁸ haben.

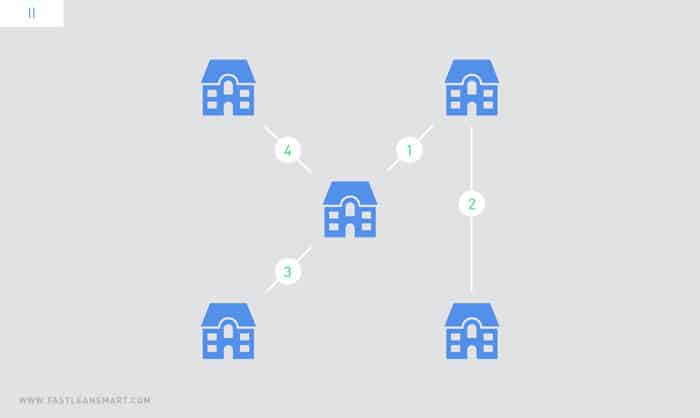
Die Bestimmung eines minimal spannenden Baums ist (je nach gewünschtem Grad der Parallelisierbarkeit) durch die Algorithmen von Borůvka⁹ bzw. Sollin¹⁰, Prim¹¹ oder Kruskal¹² effizient möglich. Fig. 2 zeigt einen MST mit Kosten 10 für den Graphen aus Fig. 1.

Fig. 2: Minimum Spanning Tree für den Graphen aus Fig. 1

Schließlich stellen wir noch durch die Dreiecksungleichung eine Anforderung an die Distanzen. Für alle Knoten a, b und c soll die Distanz zwischen a und b nicht größer sein als die Summe der Distanzen von a nach c und c nach b. Intuitiv bedeutet das, dass die direkte Verbindung zwischen zwei Knoten immer eine minimale Distanz¹³ hat. Dies ist in der Praxis aber typischerweise der Fall.

3. EIN APPROXIMATIONSALGORITHMUS

Was haben nun ein MST (der effizient berechnet werden kann) und eine optimale Tour (bei der dies nicht der Fall ist¹⁴) miteinander zu tun? Zunächst halten wir drei Beobachtungen fest:

1. Aus einer Tour lässt sich durch Entfernen einer Kante ein Teilgraph herstellen, der kreisfrei und zusammenhängend ist und alle Knoten enthält. Ein solcher Teilgraph ist ein spannender Baum. Seine Gesamtlänge kann nicht kleiner sein als die eines minimal spannenden Baums.

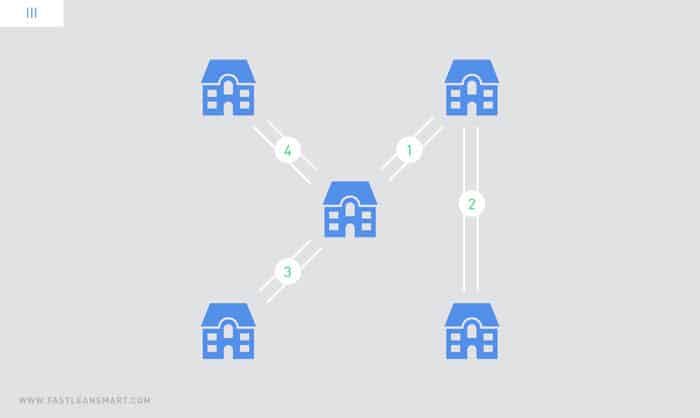
2. Aus einem spannenden Baum lässt sich eine Tour herstellen, in der Knoten mehrfach besucht werden dürfen. Dazu traversieren wir den spannenden Baum so, dass jede Kante zweimal verwendet wird. Die Gesamtlänge, der so entstehenden Tour, ist das Doppelte der Gesamtlänge des zugrundeliegenden spannenden Baums. Fig. 3. zeigt eine solche Tour mit Kosten 20 für den MST aus Fig. 2.

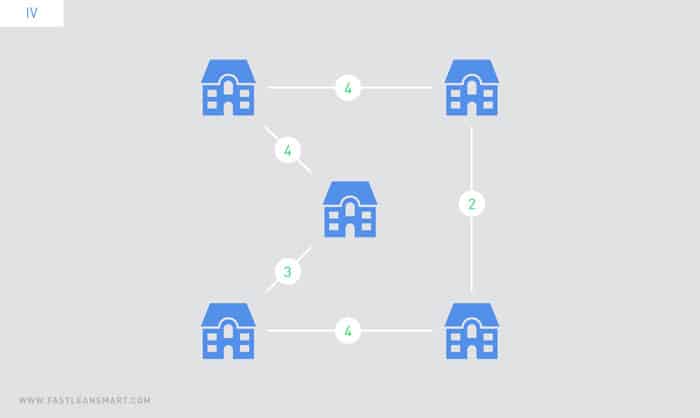
3. Aufgrund der vorausgesetzten Dreiecksungleichung wird eine wie in 2. ermittelte Tour nicht länger, wenn an einem beliebigen Knoten gestartet wird und bereits besuchte Knoten übersprungen werden. Fig. 4 zeigt eine solche aus dem MST in Fig. 3 gewonnene Tour mit Kosten 17.

Fig. 3: Durch geeignete Traversierung gewonnene Tour für den Minimum Spanning Tree aus Fig. 2

Fig. 4: Durch Anwendung der Dreiecksungleichung gewonnene Tour für Fig. 3

Diese Bausteine bilden die Basis eines Algorithmus, der die Bestimmung einer Tour bei Eingaben mit Dreiecksungleichung innerhalb einer Approximationsgüte von 2 löst. Dabei wird zuerst ein minimal spannender Baum ermittelt; wegen 1. kann dessen Gesamtlänge nicht größer sein als die Gesamtlänge einer kürzesten Tour. Mit der Konstruktion aus 2. wird dann eine Tour ermittelt – diese ist zwar keine zulässige Lösung für die TSP-Instanz, da Knoten mehrfach besucht werden können; die Gesamtlänge hat sich allerdings höchstens verdoppelt, was sich aber noch innerhalb des Rahmens der angestrebten Approximationsgüte von 2 bewegt.

Schließlich wird aus der so erzeugten Tour noch mit 3. eine Tour ohne Knotenwiederholungen gewonnen, indem bereits besuchte Knoten entfernt werden. Dadurch kann wegen der Dreiecksungleichung die Tour nicht mehr länger werden, was insgesamt die Approximationsgüte von 2 einsichtig macht. Fig. 5 zeigt eine optimale Tour mit Kosten 16 für den Graphen aus Fig. 1. Dies zeigt auch, dass der vorgestellte Algorithmus nicht immer eine optimale Tour erzeugt.

Fig. 5: Optimale Tour für den Graphen aus Fig. 1

4. FAZIT

In diesem Artikel haben wir gesehen, dass das TSP mit Dreiecksungleichung durch einen Approximationsalgorithmus mit Güte 2 lösbar ist. Neben wenigen weiteren Details ist die Hauptzutat ein Algorithmus zur Bestimmung eines MST. Das Erlauben von Knotenwiederholungen ist ähnlich wie bei anderen Problemen in der Logistik und im Field Service Management eine Relaxierung, da durch Abschwächung einer Nebenbedingung zu einer Obermenge der zulässigen Lösungen übergegangen wird.

Durch die Dreiecksungleichung wird dadurch das Optimum allerdings nicht besser; wir zielen auch nicht darauf ab, die Relaxierung optimal zu lösen. Stattdessen erzeugen wir eine zulässige Lösung der Relaxierung, deren Zielfunktionswert sich innerhalb eines konstanten Faktors des Optimums des Ausgangsproblems bewegt.

Zusätzlich zu einem MST kann noch ein kardinalitätsmaximales Matching¹⁵ in allgemeinen Graphen verwendet werden, um eine Approximationsgüte von 3/2¹⁶ zu erhalten. Dieses kann effizient mit dem Algorithmus von Edmonds¹⁷ berechnet werden.

Weitere Artikel:
➡ TOPOLOGISCHE SORTIERUNG
➡ DAS RUCKSACKPROBLEM
➡ DYNAMISCHE PROGRAMMIERUNG
➡ GANTT CHARTS IN DER TOURENPLANUNG

Karriere & Jobs:
Du bist Student:in oder Absolvent:in und interessierst dich für logistische Problemstellungen oder für die Softwareentwicklung? Dann warten bei FLS und in der Solvares Group spannende Aufgaben auf dich. Schau dich auf unserem Karriereportal nach aktuellen Stellenangeboten um oder bewirb dich einfach initiativ:

GEMEINSAM ETWAS BEWEGEN

Moin-Kultur meets Morgen-Technologie. Jetzt aktuelle Jobangebote entdecken.

ZUM KARRIERE-PORTAL

Anmerkungen:

^{1 gewidmet Oliver Graack zur zehnjährigen Firmenzugehörigkeit

2 Damit ist eine Reihenfolge der Knoten gemeint, in der jeder Ort genau einmal vorkommt. Wir unterstellen, dass nach Erreichen des letzten Knotens wieder auf direktem Wege zum ersten Knoten zurückgekehrt wird.

3 Möglichweise wird dabei der gleiche Knoten mehrfach besucht. Es handelt sich dann aber dennoch um eine Besuchsreihenfolge mit minimaler Gesamtdistanz, die somit als Lösung des tatsächlichen Tourenplanungsproblems anzusehen ist.

4 Thomas H. Cormen, Charles E. Leiserson, Ronald R. Rivest: Introduction to Algorithms,
MIT Press, McGraw-Hill, 1990.

5 Edsger W. Dijkstra: A note on two problems in connexion with graphs,
Numerische Mathematik 1959, 1:269–271, 7. Algorithmus der Woche im Informatik-Jahr 2006.

6 Robert Sedgewick: Algorithmen, Addison-Wesley, 514–524, 1991.

7 Diese durchaus übliche Terminologie reizt zu der scherzhaften Bemerkung, dass ein Baum genau dann minimal spannend ist, wenn er maximal langweilig ist.

8 Die Motivation aus dem Straßenbau (die zudem hier noch monokriteriell beschrieben wird) dient in erster Linie der thematischen Konsistenz. Natürlich ist die Minimierung der Gesamtlänge eines Straßennetzes allein kein geeignetes Kriterium, um eine Planung zu bewerten – vielmehr sollten geographische Faktoren ebenfalls Berücksichtigung finden. Wesentlich realistischer ist allerdings eine Anwendung in der Planung der Verlegung von Leitungen, beispielsweise für Versorgung mit Elektrizität oder kabelgebundene Kommunikationsnetzwerke.

9 Otakar Borůvka: O jistém problému minimálním, Práce mor. přírodověd. spol. v Brně III, 1926, 3:37–58.

10 M. Sollin: Le trace de canalisation, Programming, Games, and Transportation, 1965.

11 Robert C. Prim, Shortest connection networks and some generalizations, Bell System Technical Journal 36, 1957, 6:1389–1401. 21. Algorithmus der Woche im Informatik-Jahr 2006.

12 Joseph B. Kruskal, On the shortest spanning subtree of a graph and the traveling salesman problem, Proceedings of the American Mathematical Society 7, 1956, 48–50.

13 Der Name „Dreiecksungleichung“ ist geometrisch motiviert; in jedem Dreieck ist die Länge jeder Seite beschränkt durch die Summe der Längen der anderen beiden Seiten. Unter „Distanz“ ist hier ggf. „Fahrzeit“ statt „Weglänge“ zu verstehen; aus beiden Metriken resultiert aber das gleiche Optimierungsproblem.

14 Außer es gilt P=NP, aber das weiß man leider nicht: https://tinyurl.com/ya6693wv

15 Ein Matching bzw. eine Paarung von Knoten ist eine Auswahl von Kanten, von denen je zwei keinen gemeinsamen Knoten haben.

16 Nicos Christofides: Worst case analysis of a new heuristic for the traveling salesman problem,
Report 388, Graduate School of Industrial Administration, Carnegie Mellon University, 1976.

17 Jack Edmonds: Paths, trees, and flowers, Canadian Journal of Mathematics 17, 1965, 3:449–467.}